Тестовое задание на ML инженера

В данном посте рассматривается тестовое задание на позицию ML-инженера в крупную компанию, которая создает IT-решения для бизнеса.

Задание

Дана последовательность чисел \(X = [x_1, x_2, ..., x_n],\) сгенерированная по формуле: \(x_k = a\cdot \sin (\omega k + \varphi) + b\cdot k + c + \varepsilon,\) \(\varepsilon \sim \mathcal{N}(\mu = 0,\sigma^2),\) $a, \omega, \varphi, b, c$ - неизвестные параметры.

В файле train.csv набор значений $x_k$ для $k=0, 1, …, 100$.

1. Проанализируйте train.csv и определите скрытые параметры $a, \omega, \varphi, b, c$.
2. Постройте модель (можно использовать регрессию, нейросети или аналитическое решение), которая предсказывает $x_k$ для новых $k$.
3. Необходимо наиболее точно предсказать значения $x_k$ для $k=101, …, 120$. Заполните предсказанные значения для k из test.csv и сохраните в файл pred.csv.

Решение

Аналитическое решение + линейная регрессия

Проанализируем временной ряд. Для начала построим график зависимости $x_k(k)$, это позволит оценить вид зависимости и степень влияния шума на данные.

import pandas as pd 
import numpy as np 
import sklearn
import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression
from scipy.optimize import curve_fit

data = pd.read_csv('../data/train.csv')
data.head()

	k	x
0	1	2.501035
1	2	3.257858
2	3	3.551333
3	4	3.513895
4	5	3.491913

plt.plot(data['k'], data['x'])
plt.xlabel('k')
plt.ylabel('x')

Text(0, 0.5, 'x')

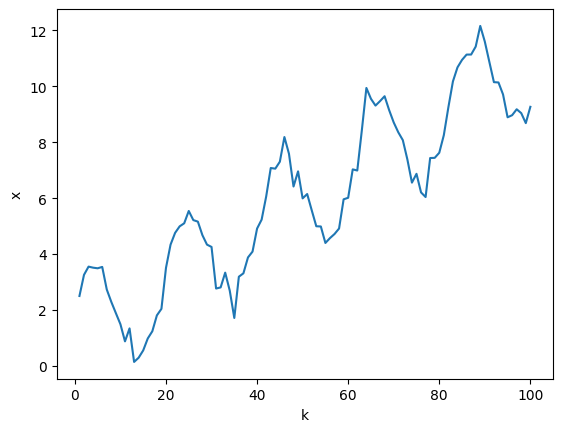
Попробуем оценить линейный тренд $x_k = b\cdot x + c + …$, превалирующий в данных, при помощи линейной регрессии.

k, x = data.k.to_numpy(), data.x.to_numpy()
model_linear = LinearRegression()
model_linear.fit(k.reshape(-1, 1), x)
b_est = model_linear.coef_[0]
c_est = model_linear.intercept_

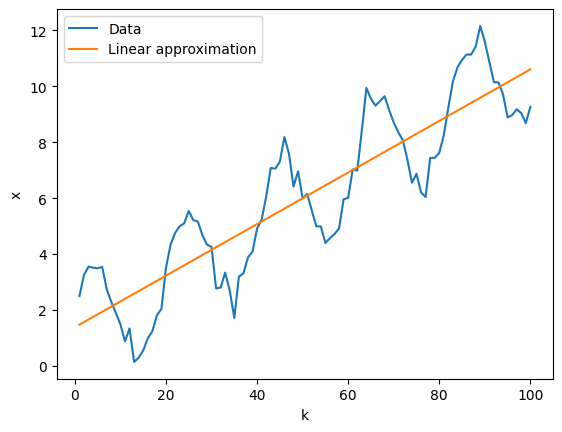
Проверяем, насколько хорошо модель линейной регрессии уловила линейный тренд:

plt.plot(k, x, label='Data')
plt.plot(k, b_est * k + c_est, label='Linear approximation')
plt.xlabel('k')
plt.ylabel('x')
plt.legend()

<matplotlib.legend.Legend at 0x17ee734d0>

Теперь можем убрать этот тренд из данных, чтобы оставить только синусоиду с шумом. После того, как мы получили синусоиду с шумом, мы можем оценить циклическую частоту при помощи преобразования Фурье. Первая гармоника будет соответствовать частоте, задаваемой синусом в формуле, так как частота сигнала сильно меньше чем частота шума.

detrended_x = x - (b_est * k + c_est)
fft_vals = np.fft.fft(detrended_x)
fft_freq = np.fft.fftfreq(len(k), d=1)[:len(k)//2] # не учитываем отрицательные частоты
pos_magnitudes = np.abs(fft_vals[:len(k)//2])

peak_index = np.argmax(pos_magnitudes[1:]) + 1
omega_est = 2 * np.pi * fft_freq[peak_index]

Проверим найденную частоту на соответствие данным визуально:

plt.plot(k, detrended_x, label='Data without linear trend')
plt.plot(np.sin(omega_est*k), label=r'$\sin(\hat{\omega}k)$')
plt.legend()
plt.xlabel('k')
plt.ylabel('x')

Text(0, 0.5, 'x')

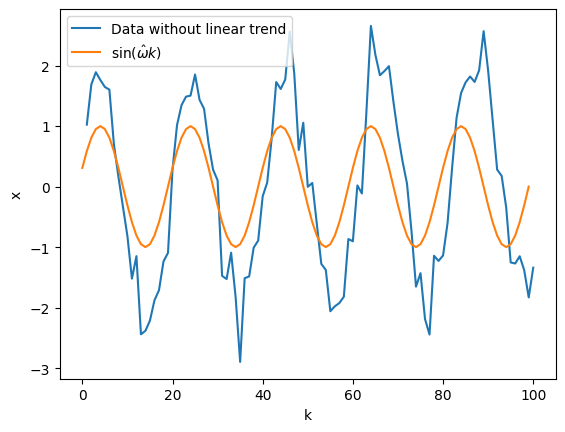
Видно, что частота оценена адекватно. Оценим оставшиеся параметры ($a, \varphi$) при помощи метода наименьших квадратов для нелинейных функций, реализованный в библиотеке scipy.

def sine_func(x, A, phi, omega):
    return A * np.sin(omega * x + phi)

(a_est, phi_est), _ = curve_fit(lambda x, A, phi: sine_func(x, A, phi, omega_est), 
                      k, detrended_x, p0=[np.std(detrended_x), 0])

params = {'a': a_est, 
          'omega': omega_est,
          'phi': phi_est,
          'b': b_est,
          'c': c_est}
params

{'a': np.float64(1.861063442722784),
 'omega': np.float64(0.3141592653589793),
 'phi': np.float64(-0.2095447762713005),
 'b': np.float64(0.09225141332626072),
 'c': np.float64(1.383491958650259)}

Оценим ошибку на обучающем наборе данных:

x_estimated = a_est*np.sin(omega_est*k + phi_est) + b_est*k + c_est
print('MSE train: ', sklearn.metrics.mean_squared_error(x, x_estimated))
print('MAPE train: ', sklearn.metrics.mean_absolute_percentage_error(x, x_estimated))

MSE train:  0.41625726203508207
MAPE train:  0.23399256878504793

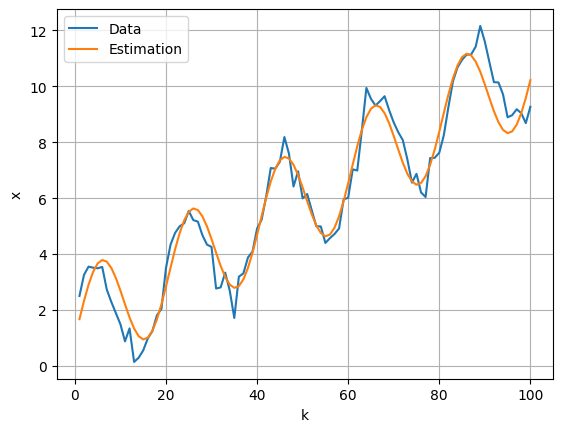
plt.plot(k, x, label='Data')
plt.plot(k, x_estimated, label='Estimation')
plt.xlabel('k')
plt.ylabel('x')
plt.grid()
plt.legend()

<matplotlib.legend.Legend at 0x2871a34d0>

Напишем функцию для построения предсказаний:

def predict_x(k_values, params):
    a = params['a']
    omega = params['omega']
    phi = params['phi']
    b = params['b']
    c = params['c']
    return a * np.sin(omega * k_values + phi) + b * k_values + c

test_df = pd.read_csv('../data/test.csv')
test_df['x'] = predict_x(test_df['k'].values, params)
# Сохраняем результат
test_df[['k', 'x']].to_csv('../data/pred.csv', index=False)

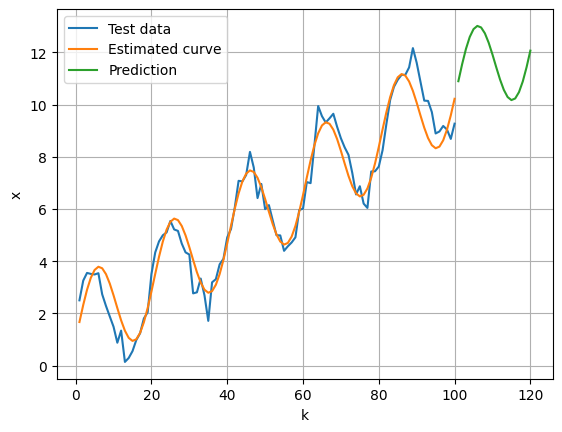
plt.plot(k, x, label='Test data')
plt.plot(k, x_estimated, label='Estimated curve')
plt.plot(test_df['k'], test_df['x'], label='Prediction')

plt.xlabel('k')
plt.ylabel('x')
plt.legend()
plt.grid()